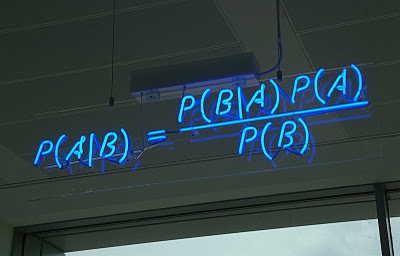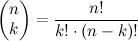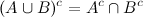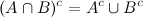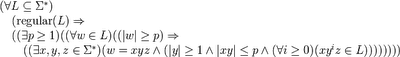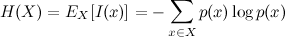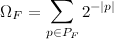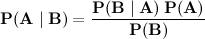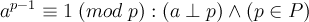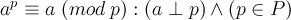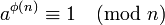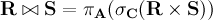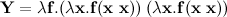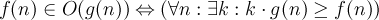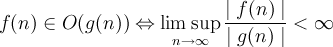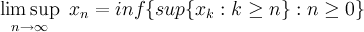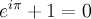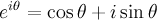Доброго вечера всем нашим читателям!
Сегодня хочу затронуть тему не совсем профильную для нашего портала, однако тем не менее очень интересную. Наткнулся тут на одну статью в англоязычном интернете, и уж очень она мне понравилась. Поэтому предлагаю Вам мой ее вольный перевод.
Биномиальный коэффициент
Биномиальной теоремы. Эти идеи приписывают Паскалю, хотя некоторые моменты были известны уже в течении тысячелетий.
Весь список из 11 уравнений не содержит какого либо порядка, однако это выражение стоит непременно запомнить, потому что оно является центральным в комбинаторике, которая имеет влияние на многие области математики. Если Вы серьезно занимаетесь компьютерной наукой или сильно связанным с математикой программированием, то Вы непременно должны уметь им пользоваться и восстанавливать по памяти, даже если Вы пьяны, разбужены посреди ночи или находитесь под дулом пистолета.
Закон Деморгана
Логическая форма:
Форма множеств:
Понимать булеву алгебру очень важно для нашей профессии. А логическая форма закона Деморгана позволит вам упрощать логические выражения.
Собственные векторы и Собственные значения
Это матрица смежности и многие другие.
В последнее время линейная алгебра становится краеугольным камнем в том, что мы делаем в нашей профессии. Она активно используется в алгоритм PageRank (Google), который базируется на этом уравнении.
Лемма о накачке для регулярных языков
Ни один список предметов изучения компьютерной науки (Computer Science) не может быть полным без “лемму о накачке”.
Хотя приведенное выше выражение достаточно специфично, оно является частным случаем более общей итерационной теоремы. Все это очень важно, если Вы занимаетесь построением Звезду Клини.
Энтропия информации
Формула энтропии из теории информации Шеннона:
И, конечно, формула Колмогоровской сложностью:
Примечательно, что данная область имеет свои параллели в реальном мире (физика) в терминах вычислениями и физическим миром, включая энтропию и уравнение Больцмана.
Теорема Байеса
Из всех уравнений из списка, data-mining’е и многом другом.
Малая теорема Ферма
Эти два уравнения Малой теоремы Ферма в сущности одно и то же уравнение, просто записанное в разных формах.
Эта красивая малая теорема вфункций Эйлера:
Эта идея крайне важна для понимания алгоритмов шифрования, таких как замечательных результатов.
Естественное соединение
Естественное соединение, как и все соединения реляционной алгебры, - это композиция более общих операций: выборка (σ), Проекция (π), Декартово произведение (×), Разность множеств (-) и их объединение (∪). Естественное соединение это декартово произведение двух таблиц с выборкой одинаковых строк и удалением дубликатов.
Реляционная алгебра становится страшным зверем, когда дело доходит до алгебраических структур, однако если Вы используете SQL, то Вы уже пользуетесь ее реализацией. Так как хранение данных становится более гетерогенно, понимание этих концепций будет становится все более важным. Кроме того, реляционная алгебра имеет большое значение для общей алгебры.
Комбинатор неподвижной точки
Уже было упомянуто несколько “уравнений” теории естественных языков и теории автоматов. Поэтому не стоит обходить стороной и Y-Combinator.
Комбинатор неподвижной точки позволяет реализовать анонимную рекурсию, которая является мощной техникой программирования. Кроме того, он также участвует в более глубоких теоретических аспектах компьютерной науки и логики, как например, комбинаторная логика.
O(N)
Некоторые могут возмутится, некоторые сказать, что это совсем не формула. Однако с этим понятием связано несколько интересных выражений, вот они:
И вот еще определение (lim sup) частичного предела последовательности:
В этом выражение inf - инфимум (infimum, точная нижняя грань) и sup - супремум (supremum, точная верхняя грань), сущности важные, если Вы имеете дела с топологией.
И самое главное - O(N) это величина показывающая сложность алгоритмов!
Тождество Эйлера
Тождейство Эйлера - пожалуй одна из самых красивых формул математики.
Надо согласиться, что конкретно эта формула не имеет такого важного влияния на компьютерную науку, как другие. Однако если Вы действительно всерьез занимаетесь ей, то Вы также должны хорошо знать математику.
Кроме того, существует частный случай при θ = π (формула Эйлера):
Эти формулы используются в математике комплексный чисел, которые в свою очередь используются в анализе Фурье, который имеет некоторые применения в компьютерной науке.